模糊综合评价法是一种基于模糊数学的综合评价方法。该综合评价法根据模糊数学的隶属度理论把定性评价转化为定量评价,即用模糊数学对受到多种因素制约的事物或对象做出一个总体的评价。它具有结果清晰,系统性强的特点,能较好地解决模糊的、难以量化的问题,适合各种非确定性问题的解决。将该方法引入风电领域,适用于解决风机健康度评价,经济性分析等问题。本文通过介绍因素集,权重集,评语集,隶属度函数等基本概念,引出模型综合评价在风机领域的应用方法,为风电机组健康度分析、经济性分析等风电数字化场景提供综合评价的方法和思路。
模糊评价相关集合概念
因素集是以影响评价对象的各种因素为元素所组成的一个普通集合,通常用U表示,U=(u1,u2,…,ui),元素 ui代表影响评价对象的第i个因素,这些因素,通常都具有不同程度的模糊性。
评价集是评价者对评价对象可能做出的各种结果所组成的集合,通常用v表示,V=(v1,v2,…,vi),元素 vj代表第j种评价结果。
权重集是对因素集每个指标赋予的权重值集合,通常用A表示,A=(a1,a2,…,ai),元素ai代表因素集中第i个因素对应的权重,权重集中所有元素权重之和为1。
隶属度函数的概念
若对论域(研究的范围)U中的任一元素x,都有一个数A(x)∈[0,1]与之对应,则称A为U上的模糊集,A(x)称为x对A的隶属度。当x在U中变动时,A(x)就是一个函数,称为A的隶属函数;隶属度A(x)越接近于1,表示x属于A的程度越高,A(x)越接近于0表示x属于A的程度越低;即用取值于区间(0,1)的隶属函数A(x)表征x属于A的程度高低。
隶属度函数的确定方法主要有模糊统计法,客观尺度法,指派法三种:
(1)模糊统计法,类似于统计学中的大样本实验法,根据概念所占比例确定其对应隶属度。
(2)客观尺度法,人们用自己对模糊概念的认识和理解,或者人们对模糊概念的普遍认同来建立隶属函数。这种方法通常用于描述人们熟知、有共识的客观模糊现象,或者用于难于采集数据的情形。
(3)指派法:通过选择已有的函数模型,对应完成隶属函数的确定。
隶属度主要分为偏大型、偏小型、中间型三种,以梯形函数为例,三种隶属度函数的表达式及对应图像如下图所示:
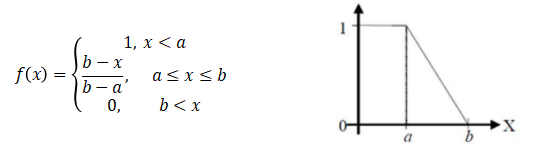
图1 梯形函数偏小型隶属度函数
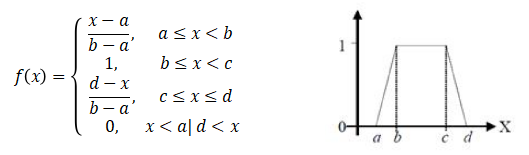
图2 梯形函数中间型隶属度函数
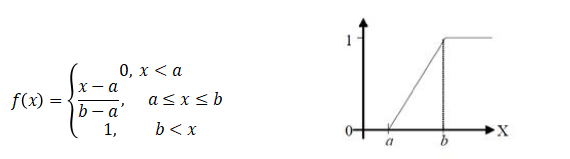
图3 梯形函数偏大型隶属度函数
模糊综合评价流程
1建立模糊综合评价的相关集合
(1)模糊综合评价的因素集
以风机健康度评价为例,选取风机运行各部件测点数据作为因素集,防止模型过于复杂,因素集选取不宜过多,并且基于相关性分析去除模型的冗余特征,降低模型复杂度。本文以皮尔逊相关系数为例讲解去除模型冗余特征的方法。
皮尔逊相关系数,也称皮尔逊积距相关系数,是一种线性相关系数,是用来反应两个变量线性相关程度的统计量,其绝对值越大表明相关程度越强。
两个变量的总体相关性系数定义为两个变量之间的协方差和标准差之积的商,通常用表示,定义如下:
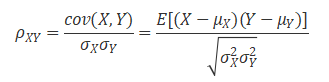
估算样本的协方差和标准差,可得到样本的皮尔逊相关系数,常用小写英文字母表示,公式如下:


r 的绝对值越大,则两变量相关性越强。若r=0,表明两个变量间不是线性相关,但可能存在其他方式的相关(比如曲线方式),两组变量的相关性图示如图4所示。
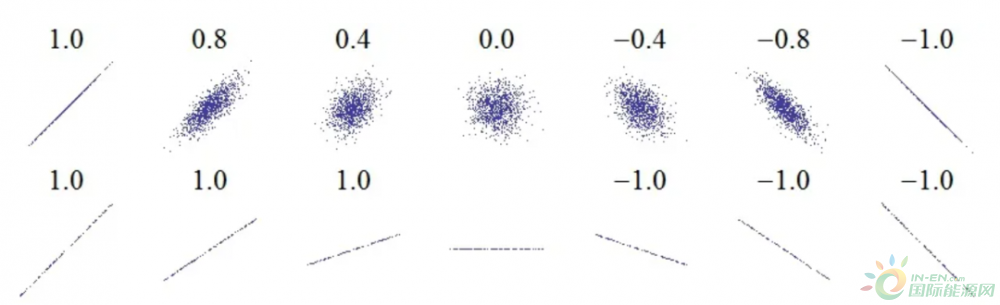
图4 样本相关性
在工程化过程中,计算两两计算特征之间的相关性系数,若相关性较高(通常以0.9以上为判定阈值),我们认为两个特征存在极强的线性关系,考虑到简化模型复杂度,减少计算量的原则,相关性较高的特征中只选取其中一个即可。
(2)模糊综合评价的权重集
权重集设置方面,主要有以层次分析法和优序图法为主的主观赋权法和以主成分分析法和因子分析法为主的客观赋权法两大类。实际落地中,我们要根据数据特点和业务需求两方面综合进行方法选择。
以主成分分析法为例,主成分分析法的算法流程如下:
1)基于PCA主成分分析算法,计算主成分的特征根矩阵E、方差解释率矩阵v,每个指标项的载荷系数矩阵C。
a)特征根可看成是主成分影响力度的指标,代表引入该主成分后可以解释平均多少个原始变量信息。一般特征根要求>1,(说明主成分的解释力度大于直接引用1个原变量)。
b)方差解释率表示提取的主成分/因子对原有变量的解释能力,方差解释率越大,解释能力越强,越能体现原始变量的关键影响因素,提取的主成分或因子越有效。
c)载荷系数解释为每个指标项对主成分的相关性系数,值域为[0,1]之间。
2)计算线性组合系数矩阵,即确定指标在各主成分线性组合中的系数,公式如下:
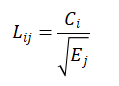
Lij: 第i个指标在第j个主成分线性组合中的系数
Ci: 第i个指标的载荷系数
Ej: 第j个主成分的特征根
3)利用主成分的方差解释率确定综合得分系数:公式为某指标与对应主成分的线性组合系数与方差解释率相乘后累加,并且除以累积方差解释率:

Si:第i个指标的综合得分系数
Lij:第i个指标在第j个主成分线性组合中的系数
Vj:第j个主成分的方差解释率
4)将综合得分系数进行归一化处理即得到各指标权重值。
(3)模糊综合评价的评价集
我们将健康程度的级别作为评价集,本文选取健康、良好、亚健康、隐患4个元素作为风机健康度评价的评价集。
2隶属度矩阵的计算
确定隶属度函数f (x),计算隶属度矩阵R:

Xij为第因素集中第i个因素在第j个评级集下的隶属度函数计算值。
3评价结果矩阵的计算
计算模糊综合评价结果矩阵:
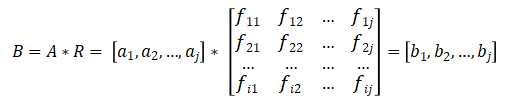
bj为评价对象在第j个评语集元素的隶属度。
4评价等级的确定
将综合评价结果矩阵转换为评价等级,评价等级可以是基于最大隶属度原则,即选取综合评价结果矩阵中隶属度最大值归属的元素作为评价结果;也可以采用加权平均法,隶属度元素平均法等方法进行评价。
以隶属度平均法为例,设限值矩阵θ=[k1,k2,…,kn],n为评价集中元素个数,将限值矩阵θ与综合评价结果矩阵点乘后得到最终分数S,再将最终分数与限值矩阵中各元素比较,归属到对应的评价等级中。
结语
模糊综合评价是对受多种因素影响的事物做出全面评价的一种十分有效的多因素决策方法。可以适用于风机健康度评估、风场经济性分析等需要对事物进行综合评价的风电数字化场景中。
模糊综合评价的流程,首先需要建立模糊综合评价的因素集、权重集、评价集。其中因素集可以基于相关性分析等方法进行降维,减小模型复杂度;权重集的设置可以用主观、客观赋权法进行设置;其次确定隶属度函数,计算隶属度矩阵,隶属度函数的确定方法主要有模糊统计法,客观尺度法,指派法三种,指派法中以梯形函数为主。然后基于模糊计算,得到模糊综合评价结果矩阵。最后将综合评价结果矩阵转化为评价得分或评级。转化的方法有加权平均法,隶属度元素平均法几种。
模糊综合评价也存在部分问题,一方面是计算复杂,并且赋权方法中主观和客观赋权各有利弊,在工程化落地中建议采用主观赋权法和客观赋权法相结合的组合赋权方法,以弥补单一赋权带来的不足;另一方面当因素集较大时,在权重集之和为1的条件约束下,相对隶属度权系数往往偏小,结果会出现超模糊现象,模型效果不足,这时可用分层评价法进行改进。
 切换行业
切换行业







 正在加载...
正在加载...




