
近年,风力发电行业的高速发展也迫切的要求提高各部件的国产化,且随着风场运维经验的增加,为各部件的国产化及优化提供了现场经验。齿轮箱作为风力发电机的核心传动部件,其故障率一直较高,特别是低速级齿轮故障。所以,系统的考虑风电齿轮箱的设计并将之系列化、标准化可以有效的提高齿轮箱可靠性,并方便维护使用。
本文从整体设计角度讨论齿形角的选择对齿轮强度的影响。
我们知道,齿轮最主要的基本参数是齿数Z、模数m、齿形角α,其基圆直径: db=mzcosα,当齿数、模数一定时,基圆直径取决于齿形角。齿形角不同,其基圆直径不同,因而其渐开线齿廓的形状也不同,所以,齿形角是决定渐开线齿形的主要原始参数之一。

图1:ISO6336方法B计算齿形系数YF的图形(来源:ISO6336-3:2006,图3)
从图1及IS06336-3:2006的齿根应力的基本值公式:
σF0=(Ft*YF*YS*YB*YDT)/(b*m)可看到,随着齿根圆角半径ρF,齿形角α,齿顶高系数ha*和模数m的变化,齿轮的强度也随之变化,合理优化这四个基本齿形参数,可以使齿轮的许用强度达到最大值(此处仅考虑了齿轮的宏观参数设计)。对于风力发电齿轮箱这样要求可靠度高、性能好且造价高的中等批量到大批量生产的产品,我们没有必要拘泥于标准中规定的值。如规定齿顶高系数ha*=1,其实这是没有任何道理的,仅仅是为了标准化的要求。所以,我们可以选取适当的值来定制刀具,这对于风电齿轮箱产品也是很经济的。
在GB/T1356和ISO53标准中都规定齿形角标准值为20°。Rankar对20°齿形角给出了如下说明:
“当发生疑问时,齿形角应取20度”这个公理,在齿轮制造者和用户之间是熟知的,但由此也不会将你引入歧途。可是,对特定的齿轮设计来说,它不是最佳的解。
所以,齿形角大于20度和小于20度各有其特点,按照风力发电齿轮箱的特点,合理选用齿形角来使齿轮的性能达到最优。
1. 齿形角对弯曲强度的影响:
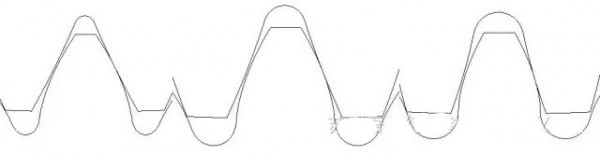
(a) (b) (c)
图2:不同齿形角的齿形比较,齿数(小轮/大轮)Z:23/104, 模数m:10, 齿形角:(a)25°; (b)20°; (c)15°
由图2可看出:随着齿形角的减小,齿轮的齿顶厚增加,齿根厚变小。齿根厚减小,齿轮的弯曲强度减小。但我们注意到随着齿形角的减小,齿轮齿根圆角半径ρF在变大,增大ρF可以有效的降低齿根应力集中系数,提高齿根的弯曲强度,通过计算我们发现:两者相互作用,齿根的弯曲强度是提高的。所以,通过增加齿形角不能有效的提高齿根强度。
这似乎与以往的文献结论不同,Beitz等人通过试验证明28º齿形角弯曲强度最高;Brugger通过封闭功率试验证明啮合角大于26º后,弯曲强度提高不明显;Niemann通过试验证明啮合角大于24º后,弯曲强度提高不明显。这个问题主要是由齿根圆角半径ρF、试验条件的不同引起的,在图2中的ρF充分利用了齿根处的空间,使用了最大的ρF值。所以优化齿根圆角可以有效的提高齿轮弯曲强度。
2. 齿形角对接触强度的影响:
从图2可看出,当齿形角增大时,齿面显得弯曲些,齿面的综合曲率半径增大,由赫兹理论可知齿面应力降低,从而齿面接触强度提高。
ГpoMaH试验表明:齿形角25º正常齿与齿形角20º变位后啮合角为25º时的齿轮弯曲强度、接触强度一样。但大齿形角齿轮会有更多的优点。
3. 齿形角对胶合强度的影响:
胶合的产生与滑动率或滑动速度有着密切的关系,滑动率大容易胶合,所以在标准ISO81400-4中推荐风电齿轮箱设计中优先考虑平衡两齿轮的最大滑动率。
从ISO21771中的计算滑动率的公式(ζ1=1-ρy2/uρy1 公式114)可推导出,滑动率是齿形角的函数,随齿形角的减小滑动率增大。
我们知道风电齿轮箱低速级通常为混合润滑,有油池飞溅和强制润滑同时存在,其润滑状态很难达到理想状态,所以容易发生胶合与微点蚀,进而引起断齿。如果在低速级适当增加齿形角,可以有效的提高胶合与微点蚀强度。同时,大齿形角容易形成油膜,这是可以理解的,当齿形角增大时齿面弯曲增加、滚动速度增加,有利于油膜的生成。
另外,如果我们减小齿顶高系数,齿顶圆直径会减小,齿轮的最大滑动率将会减小,同样也可以提高胶合强度与微点蚀强度。
4. 齿形角的其他影响:
4.1 对轴承径向力的影响:
齿轮径向力Fr=Ft*tgα,所以相对于20º齿形角,齿轮径向力改变tgα/tg20°=2.75tgα倍。例如:20°齿形角增加为25°时,齿轮径向力增加了28%,从而引起轴强度与轴承寿命的降低。
4.2 对不产生根切最少齿数Zmin的影响:
由公式Zmin=ha*/(sinα)2可知,增加齿形角可以减少不产生根切的最少齿数。








