风能是一种清洁、环保、储量巨大的可再生能源。由于风能的分布较为分散,能量密度低,因此风力发电机的工作环境较为恶劣。同时气动及流固藕合问题也相对复杂,这就对风力发电机的安全可靠性提出了很高的要求。随着对风力发电技术研究的不断深入,升力型垂直轴风力发电机越来越受到风电行业的普遍关注,其风能利用率不低于水平轴风力发电机,并且具有维护方便、适用范围广、噪音污染小和不需要偏航装置等优点。
叶片是风力发电机中最基础和最关键的部件之一,其良好的设计、可靠的质量和优越的性能是保证风力发电机稳定运行的决定因素。叶片不仅需要具有密度小、机械性能和疲劳强度好等特点,还必须能经受暴风等极端恶劣条件和随机负荷考验.叶片主要承受旋转离心力、自身重力及风对叶片表面的压力,其强度问题应得到足够的重视。
风力发电机结构分析主要包括静力分析、模态分析、疲劳寿命分析和流固耦合分析等.实验分析和有限元分析是进行结构分析常用的方法.由于实验分析方法成本较高且可行度偏低,所以风力发电机结构分析更多采用有限元分析的方法。本文将对南通大学自主研发的1kw低风速直驱型垂直轴风力发电机的叶片进行静力学分析,来检验结构设计的合理性,并为风力发电机的检测打下理论基础。样机如图1所示。

1 风力发电叶片结构
本文研究的叶片采用NACA0018翼型,其特点是:在180°攻角范围内升力和阻力特性对称,俯仰力矩系数为0,在风轮工作过程中不产生反向力矩,优势较为明显.叶片如图2所示.
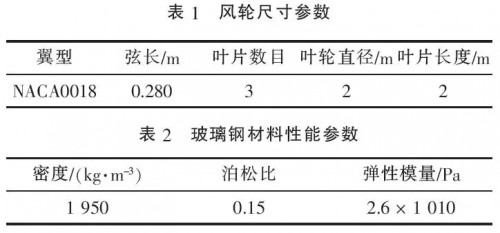
同时,为了保证叶片具有足够的强度、刚度、耐腐蚀、长寿命等性能,同时考虑到加工的难易程度、性价比高等特点,叶片的材料一般选用铝合金、玻璃钢以及碳纤维增强复合材料等制造.目前由于玻璃钢具有重量轻、强度高、性价比高等优点,已经成为风力机叶片设计的主流材料.本文研究的叶片也是采用玻璃钢材料制作而成的问,叶片尺寸参数及材料性能参数如表1,2所示.
2 风载计算
载荷分析在风力发电机的力学计算中属于一项很基础的工作,是各部件设计的前提,同时也是后期力学计算及检测的基础.垂直轴风力发电机运行环境中的载荷非常复杂,主要可以概括为空气动力载荷、重力载荷和离心力载荷口].其中重力载荷及离心力载荷均可在有限元软件中直接添加,而空气动力载荷则需要根据叶片翼型,设定工况进行计算.
2.1 计算域的划分
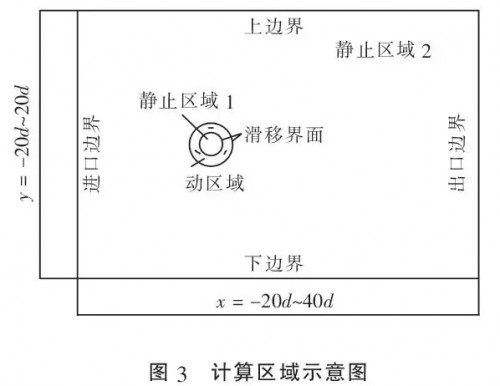
为了尽可能地节省计算机资源和时间,本文在进行模拟时尽量减小边界条件对风场的影响.选择风力发电机的中心为坐标原点,在进行边界设定时,左侧边界到原点距离是直径的20倍,右侧边界到原点距离时直径的40倍,上下边界到原点的距离也是直径的20倍.本文所研究的风力发电机的风轮直径为2 m,所以计算域在x方向上的范围为(-40, 80),在Y方向上的范围是(-40, 40),单位为m,图3为将风轮部分局部放大后的计算区域示意图.
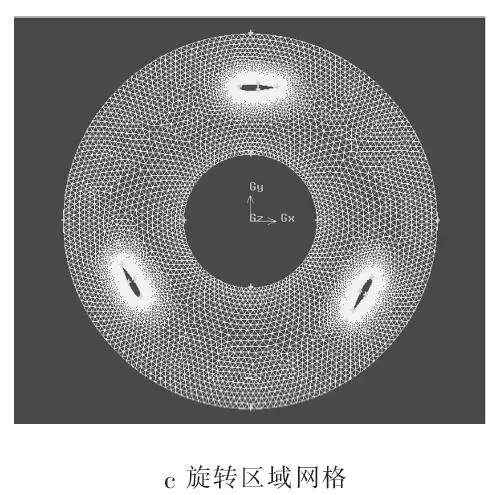
对于风轮静止区域和旋转区域之间交界面的问题,本文采用滑移网格技术来解决,即在滑移面的两侧划分不同的网格,当交界面两侧的网格存在相互滑动时,流过交界面两侧的通量相等.在非定常数值模拟中,根据已经设定好的时间步长,滑移边界按照既定转速沿着指定的方向旋转,2个滑移边界都需要经过Fluent软件中的藕合处理,才能进行计算叹
2.2 网格划分
网格的质量对数值模拟流场的结果有着极为关键的影响.网格是计算流体力学模型的几何表达式,是求解控制方程的基础,数值计算结果的收敛性和精度都受到网格质量的影响.由于叶片边界附近物理量存在较大的梯度变化,因此对叶片的边缘进行边界层处理是十分必要的.对叶片所在的动区域进行适当的网格加密处理,外部静止区域则采用较大的网格进行划分.整个流场区域均采用非结构三角形网格划分,图4为流场计算的二维网格.


 [pagebreak]
[pagebreak]
2.3 边界条件的设定
边界条件为计算域和翼型边界处的值,对Fluent模拟计算的结果有着非常大的影响.合适的边界条件不仅要求在数学上满足适应性,而且在物理上具有明显的意义.本文的边界条件设置如下:
1)进口边界 如图3所示,将方框的左边界设置为系统的速度人口边界(velocity inlet),风速设置成10 m/s,方向为水平方向向右,人口湍流方式为湍流强度比率,豁性比为10.
2)出口边界 将方框的右侧边界设为系统的压力出口边界(pressure outlet),将出口静压力设定为0 Pa,出口湍流方式采用湍流强度比率,豁性比为10.
3)壁面边界 将方框的上下两个边界和叶片边界都设置为系统的壁面边界(wall ),在壁面边界处,流体在壁面上的速度与壁面的相对速度应当为0,即不存在滑移,该壁面即称为无滑移、无渗透壁面.
4)滑移边界 将图3中动区域与静区域的交界圆面设置为系统的滑移边界(interface ) ,滑移网格技术适用于周期性问题,是计算叶轮机械非稳态问题最为精确的方法.
2.4结果分析
利用Fluent软件进行流场计算,分别得到3个叶片在流场中的压力分布云图,如图5所示,可以观察出叶片受到的最大压力约为537 Pa,位于迎风部位,即叶片前缘.
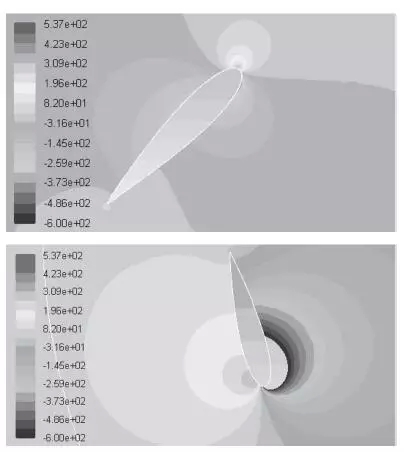

3 叶片静力分析
3.1 有限元分析基本理论
有限元分析是将大型几何结构离散为有限数量的单元体,同时利用弹性力学基本方程理论和最小势能原理对各单元联立求解,得出满足工程精度的近似结果来替代对实际结构的分析,这样可以解决很多实际工程中难以解决的复杂问题。
有限元分析是将大型几何结构离散为有限数量的单元体,同时利用弹性力学基本方程理论和最小势能原理对各单元联立求解.
对于连续弹性体,采用有限元法离散单元后,这些单元通过节点传递载荷,任意单元体的位移矢量U可以表示为

再根据整个有限元系统的力和位移边界条件,即可求取其应力分布特征。
[pagebreak]3.2有限元模型建立
3.2.1模型简化
本文研究的风力发电机叶片主体由玻璃钢材料构成,在叶片内部填充聚醋泡沫材料,并在叶片与连杆连接部位安置铝合金加强件以提高叶片与连杆连接处的强度.对于有限元分析来说。此类叶片结构较为复杂,不同种类的材料、几何尺寸都会对网格划分及计算的难度带来较大影响,且聚醋泡沫具有质量轻的特点,对计算结果的影响较小,所以在进行有限元计算时将其简化,简化后的叶片由玻璃钢壳体及铝合金加强件组成.
3.2.2有限元网格划分
叶片材料分为玻璃钢和铝,在划分网格之前将参数添加到设置中去并设置材料的特性,本文涉及到的材料均采用3D特性.本文在计算时采用mm为基础单位,这样得到的应力值与变形量的数据单位就对应着MPa和mm.
对所有有限元计算来说,单元划分的精度与计算所耗费时间的长短永远难以协调.一般来说单元的尺寸小,得到的网格密度则会更大一些,划分的网格精度随之更高,计算当然更加精确,结果更加可靠,但是对应的计算时间会变长,产生的数据库文件也相当庞大;如果单元尺寸划分较大,网格精度便会大打折扣,虽然计算时间会有所变短,但是大大降低了计算结果的精度,结果未必可靠,因此计算精度和计算时间必须进行折中.经反复验证,叶片边界网格划分精度定为10,采用六面体网格,最终得到的网格规则且均匀,一定程度上可以减小对计算精度的影响,计算时间也不至于过于冗长划分后的网格如图6所示.

划分后3个叶片总单元为29 100,节点37 269个.该有限元模型将用于下文的静力与模态分析中.风力发电机其他部件不在本文研究范围内,所以采用自动化分的方法,为了节省计算时间,网格划分精度较低.
3.2.3边界条件与载符
在网格划分的基础上,根据实际负载情况,增加了负载和边界条件.为了使计算结果更加精确,更加接近真实工况,本文在进行有限元计算时建立了整个风力发电机的模型,叶片与连接杆之间施加焊接接触,对叶片、主轴及其他部件的装配体进行力学分析.根据第二节的分析及计算,对计算模型分别施加风载、重力及旋转离心力.其中风载施加在3个叶片上,为均布载荷537 Pa;重力施加在整个模型的重心;风力发电机为逆时针旋转,施加逆时针旋转离心力,施加载荷如图7所示.

在实际的工况中,3个叶片和连接杆相连接,绕着主轴做圆周运动,主轴的下端固定,并且只能绕Z轴方向旋转.风力发电机塔架固定在基座上,所以风力发电机在X,Y,Z方向上的位移自由度全约束,如图8所示.

4 计算结果分析
叶片在给定工况下的位移场分布云图、应力云图如图9-10所示.
由仿真结果知:
1)叶片的形变从叶片与连杆连接处到叶片2个顶部是逐渐增加的,连接处形变量最小,叶片两端偏移最大,尤其是叶片后缘较薄部分,最大的变形量为31.25.
2)叶片的应力分布体现出越靠近叶片连接处,应力值越大的规律,最大应力值为69.26 MPa,均发生在叶片连接点处.

5 结论
仿真结果显示叶片最大应力约为69.26 MPa,而玻璃钢叶片静力强度许用应力为255 MPa,所以,叶片在额定工作状态下符合设计要求.叶片的受力以叶片与连杆的连接点处最大,连接点处更容易因为强度问题而发生损坏.在设计叶片时,可以适当加强连接点处的强度,同时也可以在受力较小的位置,如叶片两端以及后缘部位适当减小填充材料的的密度或采用空心结构,这样既能节省材料,也可以减轻重量。
 切换行业
切换行业







 正在加载...
正在加载...




